基準となる性能は？
エッジがあると判断している基準は【-日中騰落率】を超えれるかどうかで決めてます。
■全営業日、前場寄付きで売り、後場引けで買戻しを行った場合。(図1
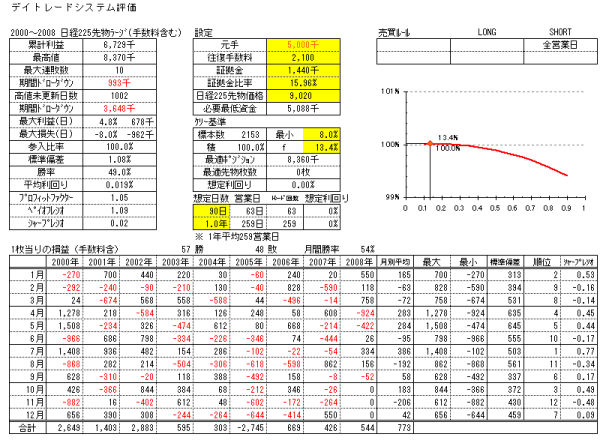
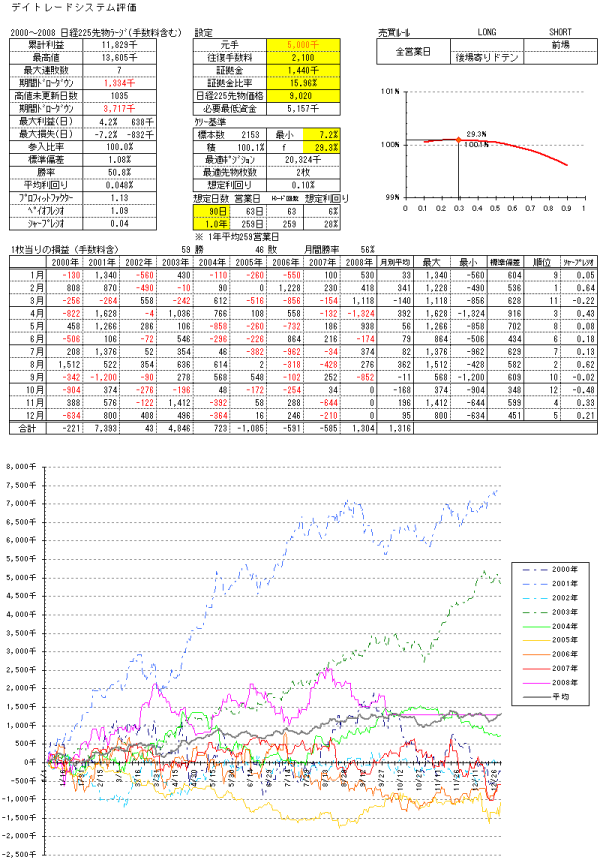
■全営業日、前場寄付きで売り、後場寄付きでドテン買い、後場引けで売却を行った場合。(図2
たったこれだけのことで
外資系注文動向のシステムと同程度の成績です。ということは外資系注文動向にはほとんどエッジがないといえます。
目標とするエッジ
僕が目標としているエッジはDOW逆張りです。これと同等のエッジが見つかれば大成功といえます。
複数の指標を組み合わせるとカーブフィッティングに陥りやすいで単独が理想ですが、乖離率や前日騰落、標準偏差や線形回帰などでは満足いく結果は得られませんでした。
条件を細かく設定すればそれなりの利益率や勝率は残せますが、累計利益が大幅に減るかカーブフィッティングとなってる可能性もでてきます。
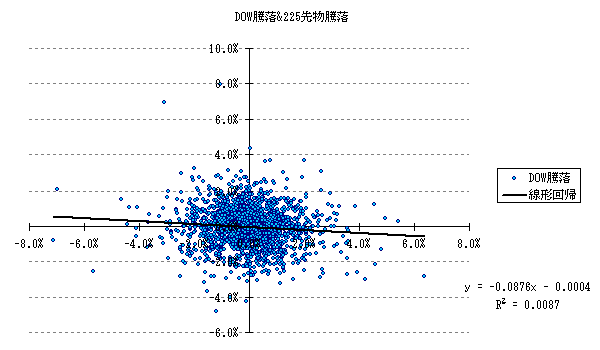
また変数が2つの場合だと、エッジを探すに散布図が便利です。R2は決定係数。
DOW騰落率と日中騰落率(図3と外資系注文動向と日中騰落率(図4を比べてみればエッジの強弱が良くわかると思います。
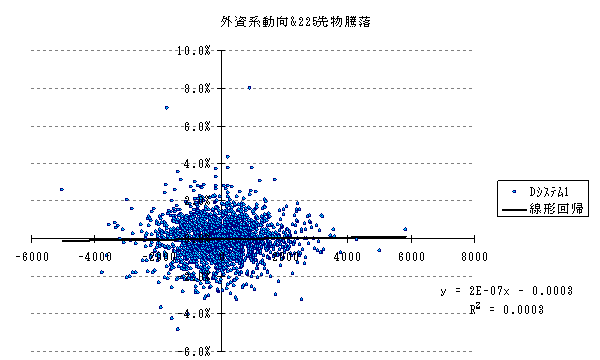
必要資金は？
先物1枚で運用した場合過去から推測できる必要資金は、期間最大ドローダウンと先物証拠金との合計になります。(ただし証拠金は株価やボラティリティで変動)
■では、ケリー基準を適用した場合はどうなるでしょうか？
(図5は
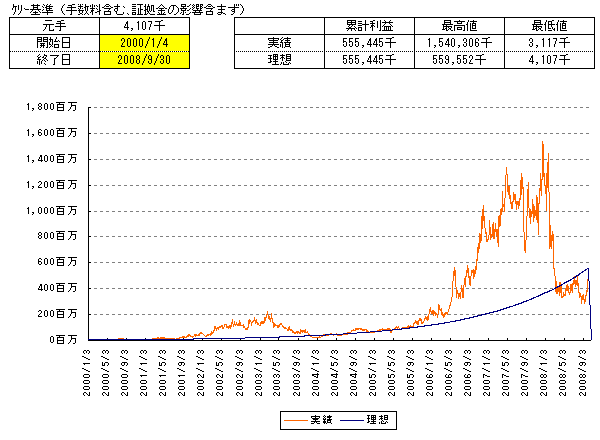
DOW逆張りシステムでの実績と理想との比較です。当初の資金は上述の必要最低資金である4,107千円としました。ただし、損益計算は最適ポジションで計算してます。(現実には不可能ですが)
この場合の最低値は3,117千となり100万円程度の含み損を抱えますが、証拠金には十分な資金が残ります。
一方、当初資金(元手)が190万を下回ってくると、最低値が現状での証拠金1,440千を下回ってきます。この場合、先物を買えなくなるので途中でリタイアとなります(実際はミニがあるので対応可能です)
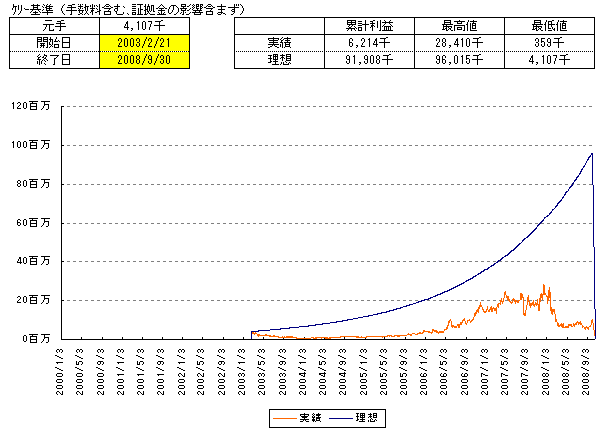
■今度は最悪期にはじめた場合を考えてみます。
(図6は高値未更新日数が380日と最悪となった時期(2003/2/21〜2004/8/6)に運用を始めた場合です。
この場合、最低値は359千となり証拠金が不足します。最低値が必要証拠金以上となるには4倍以上の元手が必要となります。現実にこれだけの資金を用意できる場合はそれで対応可能ともいえますが、今回たまたま4倍だったというだけで確実な値は存在しません。
未来は予測できないので根本的な解決策は存在しませんが、とりあえずは余剰資金を残しておく(ケリー基準を適用する金額を減らす)ことが有効と思われます。
また、ここではケリー基準の算出期間と運用期間が異なるため実績が理想の累計利益を大きく下回っています。このパターンは現実の運用では大いにありえることですが、やはり余剰資金を残しておく程度の対策しかないと思われます。
手数料の影響
現在、システムの手数料はkabu.comの往復2,100円を採用しています。
決して高くはないですがこれよりも安いところは多く存在します。ここでは日計りの返済手数料が無料(往復1,050円)となるマネックス証券と比較してみました。
※作ったあとで確認したのですがkabu.comは片道987円。ﾏﾈｯｸｽは525円(日計り返済無料)でした。
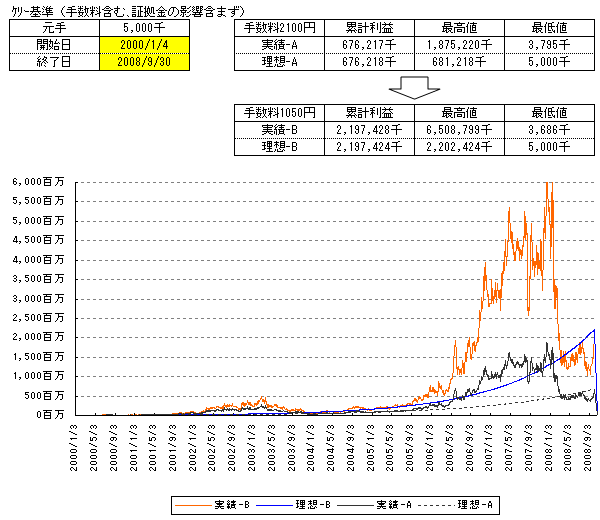
■往復手数料1,050円の場合のDOW逆張りシステム評価。(図7
売買回数の多いシステムというのもありますが、累計損益で2,169,300円(2066回×1050円)も変わってきます。
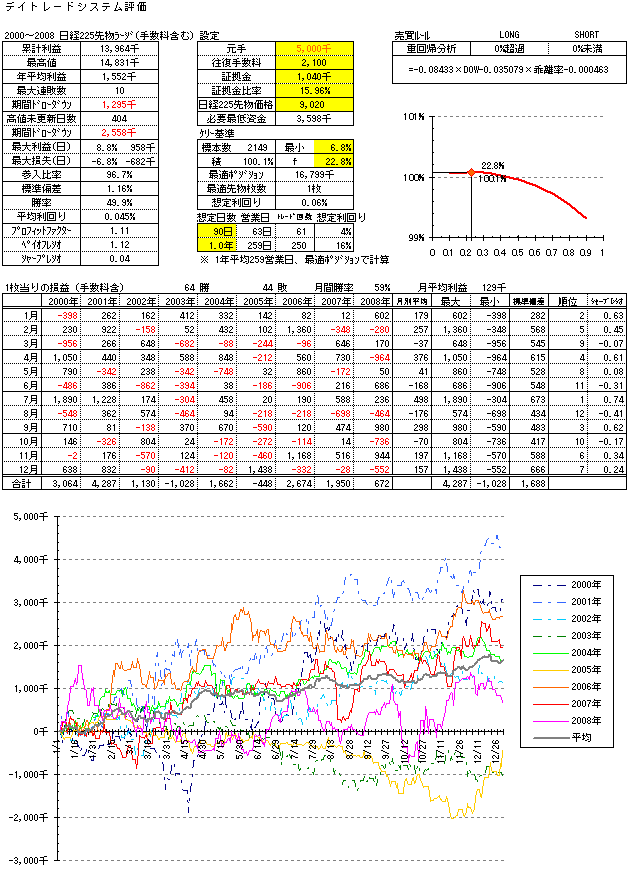
参考DOW逆張りシステム評価(手数料2100円)
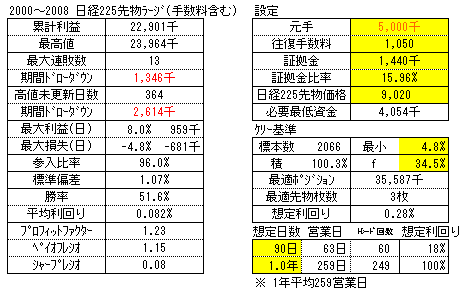
■さらに驚くべきはケリー基準を適用した場合です。（図8
複利の効果やf値の上昇もあって累計利益では3.2倍以上もの差がでてます。（元手が500万円の場合）
これは売買回数のほか平均利回りに対する手数料の割合が大きいことがあげられます。極端な例ですがわずか1,050円といえども恐ろしい効果です。
エッジの合成
複数のエッジを利用する場合、最も簡単な手法はシステム検証時に複数の条件を設定しておく方法です。
ただ、これの問題点は条件を増やすことによるカーブフィッテングや取引機会の減少が生じやすいことです。
ここではそれを避けるために重回帰分析を行ってみます。
扱う独立変数はDOW騰落率と6日移動平均乖離率とし翌日の日中騰落率を回帰分析してみます。
（ここでの移動平均線の日数は最適化されてたものではないです） 値はExcel、
重回帰分析１で実際に求めてたものを使います。
その結果、決定係数は0.0103511となり重回帰式がＹ＝−0.08433×DOW−0.035079×乖離率−0.000463（切片）と求められます。参考までにDOW騰落率単独での決定係数は0.0079811なので若干改善してます。
ちなみに回帰分析は2008年9月末時点でのデータを使用していますので、それ以降の3か月間はフォワードテストになります。
■重回帰分析による合成評価シート１（図9
次に、同じデータを使用してますがダミー変数を利用し定性的に評価した場合の回帰式です。
重回帰分析２で実際に求めたものです。
決定係数は0.011398、重回帰式がＹ＝−0.00163×X1+0.00077×X2−0.03645×乖離率-0.03645（切片）です。
■重回帰分析による合成評価シート２（図10
結果は思ったよりもよくないです。
実は決定係数の小さい、DOW騰落率のみを回帰分析した回帰式を使ったシステムの方がよい結果がでます。正確な理由はわかりませんが、DOW騰落率のエッジに比べて極端に弱い（もしくはエッジではない）ことが原因と思われます。
結果的に例題は失敗してしまいましたが、重回帰分析が有効な方法のひとつであることは確かです。
|
